|
|
|
Viewing Distance and Screen Size
In a home theater, the ideal viewing distance for a given screen size is largely a matter of personal taste. Factors such as room layout and budget considerations also enter into the equation. We can however derive a few measurements to help guide the choice of screen size and seating placement.
The concepts of screen size and viewing distance are interrelated. A 34" screen viewed from two feet away appears as large as a 100" screen viewed from 6 feet away. The reason for this is because they both fill up the same amount of our field of vision. The amount of our field of vision consumed by a screen is called the viewing angle.
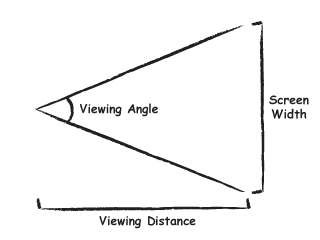
Determining Screen Width
The first step in deriving the viewing angle is determining how wide our screen is. The size of most screens is given as a diagonal and an aspect ratio. The aspect ratio is calculated by dividing the width of a screen by it's height. The aspect ratio of most standard definition sets is 1.33 (sometimes called 4:3). The aspect ratio of most HDTVs is 1.78 (sometimes called 16:9). The later is also commonly called widescreen, though the term could refer to other aspect ratios as well. The aspect ratio describes how much wider the screen is than it is high. For instance a 1.78 aspect ratio screen is 1.78 times as wide as it is high.
The width of a screen can be determined using some basic trigonometry. The screen width, height, and diagonal make up a right triangle.
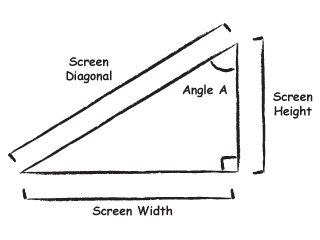
Since the the aspect ratio gives us the width divided by the height of our triangle we can calculate angle A in the diagram above by taking the arctangent of the aspect ratio.
So for 1.33 screens angle A is about 53.1 degrees and for 1.78 screens angle A is about 60.6 degrees.
Now we can calculate the screen width by multiplying diagonal by the sine of angle A. Similarly the screen height can be calculated by multiplying the diagonal by the cosine of angle A.
For a 50" 1.78 screen the width will be about 43.5" and the height will be about 24.5".
We can do this in reverse as well. Assuming we've found an appropriate screen width for our viewing distance we can calculate the diagonal by dividing the width by the sine of angle A.
Determining Viewing Angle
Now that we know the width of our screen we can use this and our viewing distance to calculate our viewing angle. The easiest way to do this is to calculate half the viewing angle from half the screen width and then double the resulting angle. This allows us to use right triangles and relatively simple math to calculate the angle.
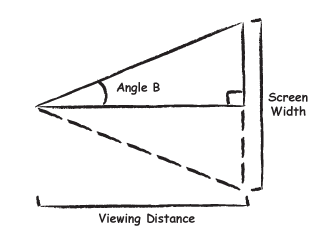
Angle B can be calculated as the arctangent of half the screen width divided by the distance. The viewing angle is then twice angle B. The units of distance and width (eg. feet, inches, etc.) don't matter as long as the units for both measurements are the same.
Half Screen = Screen Width / 2
Angle B = arctan(
Half Screen / Viewing Distance )
Viewing Angle = Angle B * 2
We can use these same basic equations in a couple other ways. Assuming we have determined a desired viewing angle we can solve for a screen width given a viewing distance.
Angle B = Viewing Angle / 2
Half Screen = Viewing Distance * tan( Angle B )
Screen Width = Half Screen * 2
Or we can solve for a viewing distance given a screen width.
Angle B = Viewing Angle / 2
Half Screen = Screen Width / 2
Viewing Distance = Half Screen / tan( Angle B )
With these equations one can try a variety of "what if" scenarios. What viewing angle would I get if I viewed a 50" screen from 6 feet? If I want a 30 degree viewing angle and have a 61" screen how far away should I sit? If I want a 40 degree viewing angle and my seating area is 8 feet away what screen size do I need?
Interpreting Viewing Angle
So now that we know how to turn a screen size and viewing distance into a viewing angle and back, the question naturally arises, what is an appropriate viewing angle? As stated there is a certain amount of subjectivity to this, but we can derive some numbers by considering viewing angle standards in commercial cinemas as well as the limits of video resolution and human visual acuity.
Widely sited research by the Japanese broadcasting company NHK found that 30 degrees is the minimum viewing angle needed to create an immersive "sensation of reality" in most viewers. The cinema certification company THX substantiates these findings by refusing to certify theaters whose viewing angle from the back row is less than 26 degrees, only 4 degrees off from the immersion angle. THX recommends that the viewing angle from the back row be 36 degrees which is comfortably within the immersion angle. The ideal viewing angle in a commercial cinema is less well defined. Anecdotally it appears that the viewing angle for an ideal seat in the middle of a cinema is about 50 degrees.
This brings us to the subject of visual acuity. A human with 20/20 vision can discern details to about 1/60th of degree. Details smaller than 1/60th of a degree cannot be discerned. This allows us to calculate some minimum viewing angles based on the resolutions of various video formats. To calculate the minimum viewing angle for a particular format we need only divide the format's horizontal resolution by 60. You will be unable to discern all the detail available in a given format if you watch from a viewing angle less than the one calculated here.
Minimum Viewing Angle = Horizontal Resolution / 60
This tells us that the minimum viewing angle for 1080p is 32 degrees. The minimum viewing angles for 720p and 480i are smaller than this, which means they're smaller than the immersion angle. It seems about 30 to 32 degrees is a pretty good minimum viewing angle for a home theater.
This bring us to the maximum viewing angle. The NHK report sets the maximum viewing angle to maintain immersion at around 100 degrees. This is of course an upper bound and most people will probably prefer to sit a bit further back than that. Additionally sitting this close to most displays will make the pixel structure far too evident, even at 1080p. At some point, individual pixels become distractingly visible. When exactly this happens depends partially on a viewer's subjectivity, but also upon the pixel structure and spot profile of a particular display. A pixel spot profile is how light is distributed across the pixel. For example, CRTs tend to have round pixels that burn brightly in the center but get dimmer at the edges. LCD projectors on the other hand tend to have square pixels that have a uniform brightness and hard edges. When the pixel structure becomes too apparent can really only be determined by observation. Finally you will find that your viewing angle is going to be limited by your minimum acceptable viewing distance. Unless you are installing a front projector you are just not going to be able to sit close enough to your display to get really large viewing angles. For example, to attain a 100 degree viewing angle one needs to sit about 2 feet away from a 71" display.
THX also certifies home theaters and for 1080p systems they recommend a 40 degree viewing angle. This is presumably higher than the immersion angle and visual acuity angle, but small enough that it is attainable, comfortable, and pixel structure will not be a distraction on most displays. THX also recommends a 30 degree viewing angle for SD. This viewing angle seems wide enough enough to reveal pixel structure on many SD displays. It was presumably chosen because no cinematic viewing angle could hide pixel structure entirely on SD sets while at the same time 30 degrees is the lowest angle that still yields some cinematic immersion.
An Example
Say you're viewing a 720p set from a distance such that it takes up 21 degrees of your viewing angle. Replacing this set with a 1080p set of the same size and sitting the same distance away will look almost identical. No significant additional detail will be revealed.
If you sit closer to the 720p set so as to get a viewing angle larger than 21 degrees, no additional information will be revealed either. The pixels will just get larger and things will appear slightly less sharp. Now imagine a 1080p set in the same situation. You can sit closer to the set and not only will your viewing angle increase, but more information will be revealed. This is until you get to a viewing angle of about 32 degrees at which point sitting closer will only create bigger pixels.
The same effect occurs if you increase the size of the set. Again imagine you're viewing a 720p set from a distance such that it takes up 21 degrees of your viewing angle. Replacing this set with a larger 1080p set but still sitting the same distance away will increase your viewing angle and reveal more information.
There is one more consideration here. As I mentioned, 30 degrees of viewing angle is the point at which people start to consider a movie experience immersive. Therefore 1080i/p is a bit of a magic format as it's the first format to have the resolution where the visual acuity angle is within the immersion angle. In fact you can actually go a bit beyond the visual acuity angle before the pixels become distracting. For years people have been watching 720p and even SD sets at viewing angles significantly higher than their ideal angles. THX therefore recommends a slightly higher and therefore more immersive viewing angle of 40 degrees for 1080p. However, in most viewing situations it gets tricky to go much beyond a 32 degree angles without going to a front projector.
Common Screen Sizes
I have gotten a lot of requests for tables of precalculated screen sizes. I initially didn't want to put up a list of viewing distances for particular screen sizes as the temptation to take these distances as the last word on viewing angles is high. In reality selecting screen size and viewing distance is a balancing act between environment, immersion, and visual acuity. For instance I would sit much closer to a 720p set than the 21 degree viewing angle calculated below. I prefer the equations above because they give you the tools to analyze a viewing environment as opposed to giving an absolute "correct answer" for a given display.
The visual acuity angle is about 32 degrees for 1080p. To calculate the viewing distance which gives you a 32 degree viewing angle on a 16:9 set just multiply the diagonal by 1.52.
Viewing Distance = Screen Diagonal * 1.52
Viewing distances which give 32 degree viewing angles for commonly sized 1080p sets :
71" diagonal = 107.9" (9') viewing distance
67" diagonal = 101.8" (8.5') viewing distance
61" diagonal = 92.7" (7.7') viewing distance
56" diagonal = 85.1" (7.1') viewing distance
50" diagonal = 76" (6.3') viewing distance
46" diagonal = 69.9" (5.8') viewing distance
42" diagonal = 63.8" (5.3') viewing distance
A similar calculation can be done for 720p. The ideal viewing angle for a 720p set is 21 degrees. To calculate the ideal viewing distance for a 16:9 720p set just multiply the diagonal by 2.31
Viewing Distance = Screen Diagonal * 2.31
Viewing distances which give 21 degree viewing angles for commonly sized 720p sets :
71" diagonal = 164.3" (13.7') viewing distance
67" diagonal = 155" (12.9') viewing distance
61" diagonal = 141.1" (11.8') viewing distance
56" diagonal = 129.6" (10.8') viewing distance
50" diagonal = 115.7" (9.6') viewing distance
46" diagonal = 106.4" (8.9') viewing distance
42" diagonal = 97.2" (8.1') viewing distance
|
|
|
Copyright 2006 GADGETBENCH |